Shooting up

[coloradoclyde]

Smoothbores can defy physics....

Why I shot one at a target and it put a hundred holes in it, yet I only fired once....... :shocked2:

I shot a bird with a smoothbore once and the bird completely disappeared.....All that was left was a couple feathers..... I think the gun opened up a worm hole or something that the bird flew into......That's some quantum level stuff right there.... :hmm:

Yep!....Smoothbores, they can defy physics....

 

[Zonie]

Well, I might as well jump in here and confuse the issue.

Everybody seems to recognize that the pull of gravity is straight down so lets keep that in mind.

As Elnathan explained, there are three forces acting on the bullet once it leaves the barrel.
There is the kenitic energy of the moving bullet that tries to keep it going at the same speed.
There is the wind resistance that is trying to slow the bullet down and there is gravity that is trying to make the bullet fall to the earth.

Lets look at the bullet if it was fired exactly horizontally at some distance above the ground.

It is making its way toward the target but the wind is slowing it down as it flies.
Gravity is pulling the bullet straight down but because it is moving it will fall in an arc towards the ground.
In the meantime, wind is slowing the bullet down so the further downrange it travels the slower it is going. Going slower gives gravity more time to work on deflecting the bullet downward.
This creates the classic downward, parabolic flight path we all know about.

In order to get the bullet to hit the target the barrel needs to be pointed upward, relative to the sights so that the bullets fall will coincide with the amount of falling it does on its way to the target.

Now, with gravity acting only in the vertical direction if the bullet was fired horizontally, 100 percent of its effect will be used only to make the bullet fall towards the earth.

If the bullet was fired in an upward direction, some of gravity's pull will be working to make the bullet fall but some of its pull will be working to slow down the bullet.
That's why if the bullet was fired straight up, 100 percent of the gravitational force would be used to slow down the bullet and cause it to fall straight back down.

Because some of the gravity's energy on these upward shots is being used to slow down the bullet, there is less energy left to make the bullet fall towards the earth so, in any given length of time, the bullet will fall more slowly.

Because it is falling towards the earth slower, it will hit the target higher.
Because of this, one needs to aim a little lower to compensate for the slower fall.

I started to explain how the effects of gravity on the moving bullet can be calculated using the sine and the cosine of the angle above the horizon but I figured that might be carrying this a bit too far. It also made my head hurt but it boils down to the sine of the angle effects the bullets speed and the cosine of the angle effects how fast the bullet falls towards the earth.

 

[George]

Because it is falling towards the earth slower, it will hit the target higher.
Because of this, one needs to aim a little lower to compensate for the slower fall.

You are lining up with those who believe the bullet flies high because droip is less. For all practical purposes that doesn't happen. It's not the amount of drop which is the probnlem, it's the angle.

How about a look at what people smarter and more experienced than any of us have to say about this problem? Here's the transcribed discussion of shooting uphill and downhill from the first edition of the Lyman Black Powder Handbook, with the graphic and chart. Have fun.

If I disappear, it's probably because the copyright gods have snatched me.

Incline Angle
Lyman Black Powder Handbook

Page 174

C. Effects of Uphill and Downhill Shooting

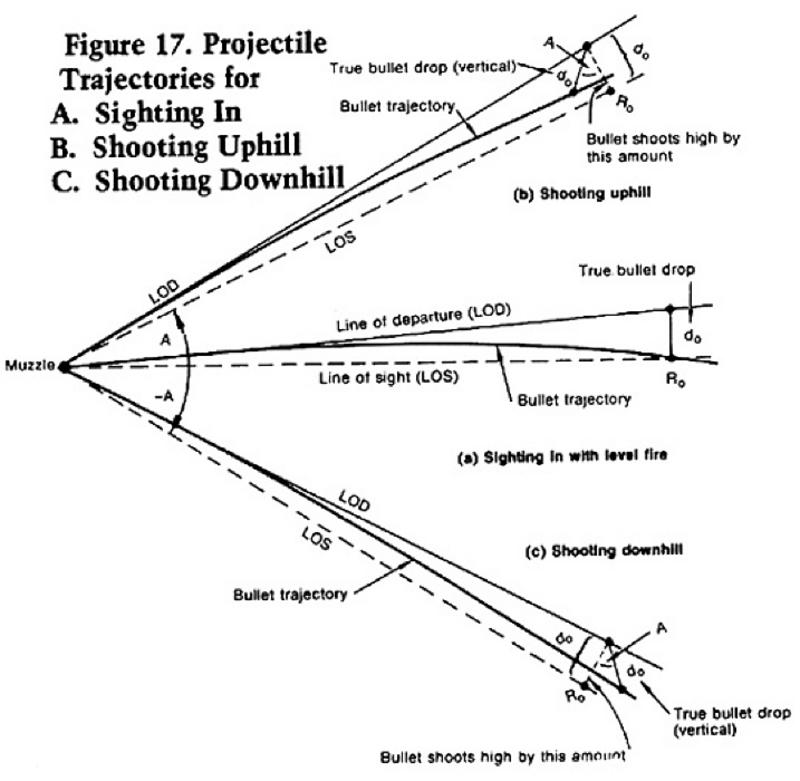
Ordinarily, a shooter will sight in a gun on a range which is nearly level. If he then happens to fire this gun at a steep angle, either uphill or downhill, the gun will shoot high. Figure 17 has been prepared to explain how this happens. It shows three cases, sighting in with level fire (Figure 17 (a)), shooting uphill (Figure 17 (b)), and shooting downhill (Figure 17 (c)).

When sighting in, the shooter adjusts his sights so that the line of sight intersects the bullet trajectory at the range called R0, which is the range where he wants the rifle zeroed in. The distance between line of departure (bore line) and the line of sight at the range R0 is the drop d0. We use this symbol to denote the amount of drop at the range where the rifle is sighted in.

Note that the angle between the bore line and the line of sight is actually very small. This angle is greatly exaggerated in Figure 17 for purposes of illustration. Even for long range shooting, it is less than one degree, and it is typically 10 to 15 minutes of arc for hunting rifles.

It so happens that, when the rifle is fired uphill or downhill, the true drop of the projectile measured at any slant range from the muzzle changes very little from the value at the same range under level fire. This is a key point. Drop, as we use the term here, is always measured in the vertical direction at the target. It is the vertical distance between the line of departure (direction of the rifle bore axis) and the bullet trajectory. Figure 17 shows how true bullet drop is measured for level, uphill, and downhill shooting situations.

It seems to be true in general that at practical ranges for hunting and target shooting the change in vertical drop with firing elevation angle is negligible even for very steep angles. Despite the fact that drop changes very little with elevation angle, the bullet path height (distance of the bullet above or below the shooter’s line of sight) does change a good deal. Consider the situation when the shooter fires a rifle uphill at a steep angle, as shown in Figure 17 (b). Since the true bullet drop changes very little, at a slant range distance of R0 from the shooter the bullet has a vertical drop essentially equal to d0, as shown in the figure. However, the line of sight at R0 still is located a distance d0 in a perpendicular direction away from the line of departure. Because of the firing elevation angle, the bullet trajectory no longer intersects the line of sight at the range R0. In fact, the bullet passes well ABOVE the line of sight at that point, as Figure 17 (b) shows. In other words, the bullet shoots HIGH from the shooter’s viewpoint as he aims the rifle, and at steep angles it may shoot high by a considerable amount, as we will show shortly.

Figure 17 © shows the situation when the shooter fires his rifle downhill. Again, the vertical drop at the slant range distance R0 changes negligibly from the value d0 for level fire, but the line of sight and line of departure still are separated by the perpendicular distance d0. The bullet again passes ABOVE the line of sight instead of intersecting it, at the range R0. Compared to the case of level fire, the bullet again shoots HIGH from the shooter’s viewpoint as he aims the rifle. Furthermore, if the rifle is fired uphill at some elevation angle, and then fired downhill at the same elevation angle, the two bullets will shoot high by almost exactly the same amount.

It is reasonably easy to calculate how much higher a rifle will shoot for any given elevation angle. To do this we need to know the bullet drop versus range for the muzzle velocity used, and we can find this in the Ballistics Tables. Let d be the bullet drop at any range R from the muzzle. The following table shows how much higher the bullet will shoot when aimed either uphill or downhill than it will when fired on a level.

Elevation Angle...Increase in Bullet Path Height

± 5 degrees”¦”¦”¦”¦”¦”¦ .004 d inches
± 10”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .015 d
± 15”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .034 d
± 20”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .060 d
± 25”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .094 d
± 30”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .134 d
± 35”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .181 d
± 40”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .234 d
± 45”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .293 d
± 50”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .357 d
± 55”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .426 d
± 60”¦”¦”¦”¦”¦”¦”¦”¦”¦”¦. .500 d

To use this table, we first look up the drop d for each value of range for our load in the Ballistics Tables. Then, we calculate the increase in bullet path height for each elevation angle of interest using the multiplying factors in the table above. This tells us how much higher the bullet will shoot than it will for level fire at each value of range and for each elevation angle we wish to consider.
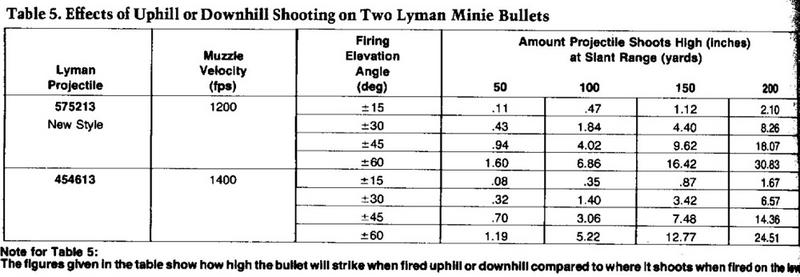
As an example of this procedure, and also to show how large an effect the firing elevation angle can have on typical projectile trajectories, Table 5 has been prepared for the two example Minnie bullets in the proceeding discussions. It is evident that either bullet will shoot several inches high when fired up or down steep inclines. The importance of understanding and compensating for firing elevation angle effects is pretty clear from these figures.

Spence

 

[Elnathan]

Thank you Spence for digging that up.

I have to point out, they do admit that there is a change in the trajectory - which I have been at pains to prove - but say that it is negligible - something that I have been saying all along is a possibility. So I think I've been vindicated here.

 

[Skychief]

If I disappear, it's probably because the copyright gods have snatched me.



Spence

You keep your cannon handy partner. Primed too. Ya hear?

 

[George]

Thank you Spence for digging that up.

I have to point out, they do admit that there is a change in the trajectory - which I have been at pains to prove - but say that it is negligible - something that I have been saying all along is a possibility. So I think I've been vindicated here.

Of course you do. Congratulations.

A change in the trajectory which is invisible doesn't get me very worked up, but that's just me.

It was no problem to dig that up. It's been part of my understanding of the problem, and on my desk, since soon after they wrote it in 1975.

Spence

 

[Skychief]

Great read and excellent illustration Spence. Should shed light on the "problem" for anyone willing to digest it. Thanks for posting this.

Best regards, Skychief

 

[George]

I originally asked if someone who subscribes to the idea that you only need to consider the horizontal distance to the target when faced with an uphill-downhill shot could explain their approach. No takers? Nobody who has actually used the idea in the field? I'd really like to understand the thinking behind that idea.

Spence

 

[Skychief]

I see that RO is what many call range of zero, (where the line of sight and trajectory meet) in the illustration. I don't see what the yardage of RO is, but doubt that it matters for the illustration's sake. Am I missing the range of RO though?

I've been known to use the "horizontal yardage hold". I don't think it's the end-all, nor perfect. I believe it works better with sights, metallic or other that ride higher of the bore versus lower. I believe as the sights get closer to the axis of the bore,or, the faster the projectile (flatter shooting), the more academic the concern becomes.

I use this "hold" with traditional archery to very good effect. My eye is basically a rear sight that is oriented 3 inches or so above the arrow (bore). Add to that the looping trajectory of a shaft versus a bullet and that may be a clue to its usefulness.

May be apples to oranges.

Back to guns ff ...Sorry... I do notice something in the illustration. If I hold a straight edge vertically along it (which should represent true horizontal distance of the slanted shots), I see that the difference between line of sight and trajectory remains fairly constant and similar at most ranges, then the gap lessens closer to RO of the "level" shot, whereas the trajectory is still above line of sight on the slanted shots at that horizontal distance.

Just some late night musings and observations.

Best regards, Skychief

PS, to say, I've noticed when my eyes were sharper, if I was hurried or in doubt about a squirrel shot, slanted of course, if I aimed at chin level or just below, it was best. This with rifles sighted in at typical squirrel shooting range to cut center right on top of the blade. What's all this mean? I dunno. :idunno:

 

[Skychief]

I should add, that it's been entirely possible that I've raised my blades a touch out of the rear's notch in the dark squirrel woods versus a sunny plinking/sighting session. Who knows.

 

[azmntman]

Thank you Spence for digging that up.

I have to point out, they do admit that there is a change in the trajectory - which I have been at pains to prove - but say that it is negligible - something that I have been saying all along is a possibility. So I think I've been vindicated here.

Of course you do. Congratulations.

A change in the trajectory which is invisible doesn't get me very worked up, but that's just me.

It was no problem to dig that up. It's been part of my understanding of the problem, and on my desk, since soon after they wrote it in 1975.

Spence

PLEASE post photo of desk :rotf: :blah:

 

[George]

:rotf:

Spence

 

[George]

I see that RO is what many call range of zero, (where the line of sight and trajectory meet) in the illustration. I don't see what the yardage of RO is, but doubt that it matters for the illustration's sake. Am I missing the range of RO though?

R0 represents the sighted-in range, the zero range, whatever it is.

Spence

 

[Skychief]

:thumbsup:

 

[Skychief]

I originally asked if someone who subscribes to the idea that you only need to consider the horizontal distance to the target when faced with an uphill-downhill shot could explain their approach. No takers? Nobody who has actually used the idea in the field? I'd really like to understand the thinking behind that idea.

Spence

Looks like you've run all your company off Spence :hmm:

 

[George]

Not a new phenomenon for me. Maybe I should take more showers?

Could it be that those who use it don't know why they do? No one would accept someone's idea about such things as gospel truth without questioning it or trying to understand it, would they? :hmm: :grin:

Spence

 

[bender20]

We had this discussion sometime back and you walked me through it then. I have since gone over the math both from the info you gave me and my own research and found it solid. No argument here.

 

[Elnathan]

Thank you Spence for digging that up.

I have to point out, they do admit that there is a change in the trajectory - which I have been at pains to prove - but say that it is negligible - something that I have been saying all along is a possibility. So I think I've been vindicated here.

Of course you do. Congratulations.

A change in the trajectory which is invisible doesn't get me very worked up, but that's just me.

It was no problem to dig that up. It's been part of my understanding of the problem, and on my desk, since soon after they wrote it in 1975.

Spence

Actually, looking at it after a bit more sleep, it looks like the chart is illustrating exactly what I was trying to get at - as elevation increases and decreases, the angle at which gravity pulls relative to the line of departure changes and the shape of the trajectory changes. The folks at Lyman explain it differently, measuring drop as parallel to the ground instead of the line of sight, but is more or less what what I was saying logically had to happen - the trajectory flattens out as the angle moves away from horizontal.

When they are talking about negligible changes in true drop, I think what they are referring to is the effects on gravity on bullet velocity and the concomitant change in trajectory from that, which would indeed be negligible.

So, yeah, I do feel vindicated, if a little embarrassed for having missed the obvious when I first read it last night. Having to rush out the door five minutes after waking up and then keep moving for 13 hours will do that, I guess...


BTW, if anyone is interested in figuring out in the "calculate drop based on the spot below the target theory," the table provided should provide the basis for testing it.

 

[George]

BTW, if anyone is interested in figuring out in the "calculate drop based on the spot below the target theory," the table provided should provide the basis for testing it.

That's the one I've been asking about. Pray do enlighten us.

Spence

 

[Elnathan]

BTW, if anyone is interested in figuring out in the "calculate drop based on the spot below the target theory," the table provided should provide the basis for testing it.

That's the one I've been asking about. Pray do enlighten us.

Spence

If you are asking about how to approach the problem, there is a beautiful, logical way to do it mathematically that is quite simple, at least for a given definition of simple. I have no idea what it is.

My redneck solution is just try it out on paper. Since the table in the Lyman handbook gives the conversion factors in multiples of 5 degrees, it seems like the best approach would be to pick a range at random and a angle for elevation - say 50 yards at 60 degrees elevation. I'd draw it out on paper as a right triangle with the bottom leg of the triangle representing the horizontal distance and the hypotenuse representing the path of the bullet to an elevated target. Think of it a paper target on the ground with a rascally squirrel (or obnoxious internet knowitall, if that suits your mood better) sitting directly above it. Use the ballistic tables in your Lyman book to calculate the drop for a given load at the distance to the ground target, then do the same for the distance elevated target modified with the conversion tables you posted above to allow for the altered angle of gravity. Compare the two figures.

I'd do that a bunch of loads, distances and angles, including a bunch of wildly unrealistic scenarios, and if the results matched up exactly or almost exactly (remember that the Lyman folks have rounded their figures to a certain number of digits) across the board, than I'd suspect that the rule was mathematically sound. If they came close but varied a bit, or if they were good for close ranges but varied considerably at further ones, I'd tend to favor the idea that it was mathematically false but useful as a rule of thumb to get you within minute of squirrel head within practical shooting distances. If they vary wildly, than it is just false and should be discarded.

Feel free to adjust the process to suit your own preferences and calculating aids available.

If you are asking me to do the math for you, 1) I must politely decline for now on the grounds I have other more pressing demands on my time and 2) I only brought up the theory (having missed its introduction to the thread earlier) as a suggestion without making any claim as to its usefulness, so while I too am interested it figuring out its validity I'm not obligated to prove anything.